（本小题满分15分）已知函数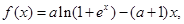
(其中
) ,
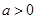点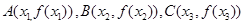
从左到右依次是函数
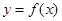图象上三点,且
.
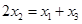(Ⅰ) 证明: 函数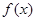
在
上是减函数；
(Ⅱ) 求证：⊿
是钝角三角形;
(Ⅲ) 试问,⊿能否是等腰三角形?若能,求⊿面积的最大值;若不能,请说明理由．
推荐套卷
（本小题满分15分）已知函数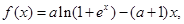(其中) ,
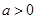点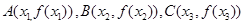从左到右依次是函数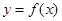图象上三点,且.
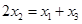(Ⅰ) 证明: 函数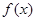在上是减函数；
(Ⅱ) 求证：⊿是钝角三角形;
(Ⅲ) 试问,⊿能否是等腰三角形?若能,求⊿面积的最大值;若不能,请说明理由．
粤公网安备 44130202000953号