（本小题满分13分）
已知函数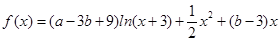
.
（1）当
且
，
时，试用含
的式子表示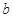
，并讨论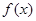
的单调区间；
（2）若
有零点，
，且对函数定义域内一切满足
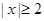的实数
有
.
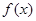①求的表达式；
②当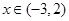
时，求函数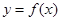
的图象与函数
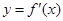的图象的交点坐标.
皆为锐角，且
，求
的值．
；
．
的定义域．
，求
的值．
的图象的一段，求其解析式．
推荐套卷
（本小题满分13分）
已知函数.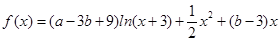
（1）当且，时，试用含的式子表示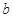，并讨论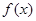的单调区间；
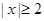（2）若有零点，，且对函数定义域内一切满足的实数有.
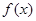①求的表达式；
②当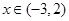时，求函数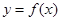的图象与函数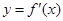的图象的交点坐标.
粤公网安备 44130202000953号