一次函数 的图象经过点
的图象经过点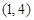 ,且分别与
,且分别与 轴、
轴、 轴交于点
轴交于点 、
、 .
.
点
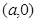 在
在 轴正半轴上运动,点
轴正半轴上运动,点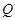
 在
在 轴正半轴上运动,且
轴正半轴上运动,且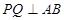 .
.(1)求
 的值,并在给出的平面直角坐标系中画出该一次函数的图象;
的值,并在给出的平面直角坐标系中画出该一次函数的图象;(2)求
 与
与 满足的等量关系式.
满足的等量关系式.
相关知识点
推荐套卷
一次函数 的图象经过点
的图象经过点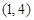 ,且分别与
,且分别与 轴、
轴、 轴交于点
轴交于点 、
、 .
.
点
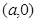 在
在 轴正半轴上运动,点
轴正半轴上运动,点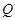
 在
在 轴正半轴上运动,且
轴正半轴上运动,且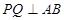 .
.(1)求
 的值,并在给出的平面直角坐标系中画出该一次函数的图象;
的值,并在给出的平面直角坐标系中画出该一次函数的图象;(2)求
 与
与 满足的等量关系式.
满足的等量关系式.