有足够多的长方形和正方形的卡片,如下图. 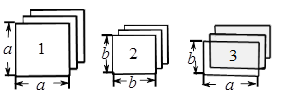
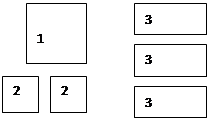

(1)如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙).请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形的代数意义.这个长方形的代数意义是 .
(2)小明想用类似的方法解释多项式乘法 ,那么需用2号卡片 张,3号卡片 张.
,那么需用2号卡片 张,3号卡片 张.
有足够多的长方形和正方形的卡片,如下图. 


(1)如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙).请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形的代数意义.这个长方形的代数意义是 .
(2)小明想用类似的方法解释多项式乘法 ,那么需用2号卡片 张,3号卡片 张.
,那么需用2号卡片 张,3号卡片 张.