某饰品店店老板去批发市场购买新款手链,第一次购手链共用100元,按该手链的定价2.8元现售,并很快售完.由于该手链深得年轻人喜爱十分畅销,第二次去购手链时,每条的批发价已比第一次高0.5元,共用去了150元,所购数量比第一次多10条.当这批手链售出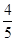 时,出现滞销,便以定价的5折售完剩余的手链,试问该老板第二次售手链是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?,若赚钱,赚多少?
时,出现滞销,便以定价的5折售完剩余的手链,试问该老板第二次售手链是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?,若赚钱,赚多少?
某饰品店店老板去批发市场购买新款手链,第一次购手链共用100元,按该手链的定价2.8元现售,并很快售完.由于该手链深得年轻人喜爱十分畅销,第二次去购手链时,每条的批发价已比第一次高0.5元,共用去了150元,所购数量比第一次多10条.当这批手链售出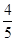 时,出现滞销,便以定价的5折售完剩余的手链,试问该老板第二次售手链是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?,若赚钱,赚多少?
时,出现滞销,便以定价的5折售完剩余的手链,试问该老板第二次售手链是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?,若赚钱,赚多少?