为了参加广州亚运会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源人数如下表:
| 队别 |
北京 |
上海 |
天津 |
八一 |
| 人数 |
4 |
6 |
3 |
5 |
(1)从这18名队员中随机选出两名,求两人来自同一支队的概率;
(2)中国女排奋力拼搏,战胜韩国队获得冠军.若要求选出两位队员代表发言,设其中来自北京队的人数为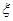 ,求随机变量
,求随机变量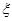 的分布列及数学期望
的分布列及数学期望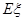 .
.
推荐套卷
为了参加广州亚运会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源人数如下表:
| 队别 |
北京 |
上海 |
天津 |
八一 |
| 人数 |
4 |
6 |
3 |
5 |
(1)从这18名队员中随机选出两名,求两人来自同一支队的概率;
(2)中国女排奋力拼搏,战胜韩国队获得冠军.若要求选出两位队员代表发言,设其中来自北京队的人数为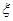 ,求随机变量
,求随机变量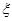 的分布列及数学期望
的分布列及数学期望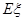 .
.