本题满分16分）
如图，抛物线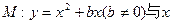
轴交于O，A两点，交直线
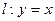于O，B两点，经过三点O，A，B作圆C。
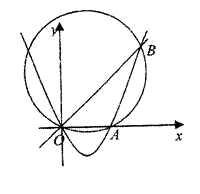
（I）求证：当b变化时，圆C的圆心在一条定直线上；
（II）求证：圆C经过除原点外的一个定点；
（III）是否存在这样的抛物线M，使它的顶点与C的距离不大于圆C的半径？
相关试题
的前n项和为
，且满足
．
，数列
的前n项和为
，求证：
．
中，M，N，G分别是
，
，AD的中点，求证：
．
，
且
．
的最大值．
；
．
．
，直线l的极坐标方程为2ρcosθ+ρsinθ-2=0．
，求过线段
的中点且与l垂直的直线的极坐标方程．相关知识点
推荐套卷
本题满分16分）
如图，抛物线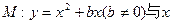轴交于O，A两点，交直线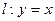于O，B两点，经过三点O，A，B作圆C。
（I）求证：当b变化时，圆C的圆心在一条定直线上；
（II）求证：圆C经过除原点外的一个定点；
（III）是否存在这样的抛物线M，使它的顶点与C的距离不大于圆C的半径？
粤公网安备 44130202000953号