（本小题满分l3分）某大学志愿者协会有6窑男同学，4名女同学，在这10名同学中，3名同学自数学学院，其余7名同学
自物理、化学等其他互不相同的7个学院，现从这10名同学中随机选取3名同学，到希望小学进行支教活
动（每位同学被选到的可能性相同）．
（1）求选出的3名同学是自互不相同学院的概率：
（2）设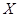
为选出的3名同学中女同学的人数，求随机变量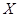的分布列和数学期望．
相关试题
求证：
且
，求证：
时,求不等式
的解集; 
恒成立,求
的取值范围.
中，底面
是正方形, 
,
分别为
的中点,且
.
;
所成的角的余弦值
.
.
(1－a)x2－3ax＋1，a＞0．推荐套卷
（本小题满分l3分）某大学志愿者协会有6窑男同学，4名女同学，在这10名同学中，3名同学自数学学院，其余7名同学
自物理、化学等其他互不相同的7个学院，现从这10名同学中随机选取3名同学，到希望小学进行支教活
动（每位同学被选到的可能性相同）．
（1）求选出的3名同学是自互不相同学院的概率：
（2）设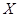为选出的3名同学中女同学的人数，求随机变量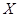的分布列和数学期望．
粤公网安备 44130202000953号