（本小题满分12分）
如图，正方形ABCD、ABEF的边长都是1，而且平面ABCD、ABEF互相垂直，点M在AC上移动，点N在BF上移动，
若CM＝BN＝a（0＜a＜
）．
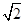（1）求MN的长；
（2）当a为何值时，MN的长最小；
（3）当MN的长最小时，求面MNA与面MNB所成的二面角的余弦值．
的前
项和
（1）求数列
，记数列{
}的前
，求
和
，求∠A和
B 的值。
的不等式
的解集为
求
的值；
，求
满足：
且
，求
的取值范围。
推荐套卷
（本小题满分12分）
如图，正方形ABCD、ABEF的边长都是1，而且平面ABCD、ABEF互相垂直，点M在AC上移动，点N在BF上移动，若CM＝BN＝a（0＜a＜）．
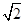（1）求MN的长；
（2）当a为何值时，MN的长最小；
（3）当MN的长最小时，求面MNA与面MNB所成的二面角的余弦值．
粤公网安备 44130202000953号