某市的老城区改造建筑用地平面示意图如图所示.经规划调研确定,老城区改造规划建筑用地区域可近似为半径是R的圆面.该圆的内接四边形ABCD是原老城区建筑用地,测量可知边界AB=AD=4万米,BC=6万米,CD=2万米.
(I)请计算原老城区建筑用地ABCD的面积及圆面的半径R的值;
(II)因地理条件的限制,边界AD、CD不能变更,而边界AB、BC可以调整.为了提高老城区改造建筑用地的利用率,请在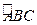 上设计一点P,使得老城区改造的新建筑用地APCD的面积最大,并求出其最大值.
上设计一点P,使得老城区改造的新建筑用地APCD的面积最大,并求出其最大值.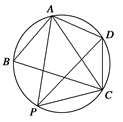
推荐套卷
某市的老城区改造建筑用地平面示意图如图所示.经规划调研确定,老城区改造规划建筑用地区域可近似为半径是R的圆面.该圆的内接四边形ABCD是原老城区建筑用地,测量可知边界AB=AD=4万米,BC=6万米,CD=2万米.
(I)请计算原老城区建筑用地ABCD的面积及圆面的半径R的值;
(II)因地理条件的限制,边界AD、CD不能变更,而边界AB、BC可以调整.为了提高老城区改造建筑用地的利用率,请在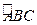 上设计一点P,使得老城区改造的新建筑用地APCD的面积最大,并求出其最大值.
上设计一点P,使得老城区改造的新建筑用地APCD的面积最大,并求出其最大值.