(本小题满分14分)
设数列{an}的前n项和为Sn,已知a1=1,且an+2SnSn-1=0(n≥2),
(1)求数列{Sn}的通项公式;
(2)设Sn=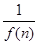 ,bn=f(
,bn=f(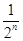 )+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn<
)+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn<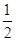 .
.
推荐套卷
(本小题满分14分)
设数列{an}的前n项和为Sn,已知a1=1,且an+2SnSn-1=0(n≥2),
(1)求数列{Sn}的通项公式;
(2)设Sn=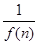 ,bn=f(
,bn=f(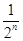 )+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn<
)+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn<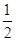 .
.