已知抛物线
和点
，过点P的直线
与抛物线交与
两点，设点P刚好为弦
的中点。
（1）求直线的方程
（2）若过线段上任一
（不含端点）作倾斜角为
的直线交抛物线于
，类比圆中的相交弦定理，给出你的猜想，若成立，给出证明；若不成立，请说明理由。
（3）过P作斜率分别为
的直线
，
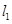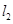交抛物线于，
交抛物线于
，是否存在使得（2）中的猜想成立，若存在，给出
满足的条件。若不存在，请说明理由。
相关试题
上的函数
(其中
).
的值；
的不等式
.
的顶点
、
、
，
边上的中线所在直线为
.
关于直线
满足：
，定义域为
的函数
是奇函数．求：
，
的值；
，不等式
恒成立，求实数
的取值范围．
是
的极值点，求
上的最小值和最大值；
上是增函数，求实数
的取值范围．
的准线的方程为
，过点
作倾斜角为
的直线
交该抛物线于两点
，
．求：（1）
的值；（2）弦长
推荐套卷
已知抛物线和点，过点P的直线与抛物线交与两点，设点P刚好为弦的中点。
（1）求直线的方程
（2）若过线段上任一（不含端点）作倾斜角为的直线交抛物线于，类比圆中的相交弦定理，给出你的猜想，若成立，给出证明；若不成立，请说明理由。
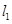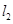（3）过P作斜率分别为的直线，交抛物线于，交抛物线于，是否存在使得（2）中的猜想成立，若存在，给出满足的条件。若不存在，请说明理由。
粤公网安备 44130202000953号