【2015高考北京，理16】
，
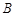两组各有7位病人，他们服用某种药物后的康复时间（单位：天）记录如下：
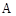组：10，11，12，13，14，15，16
组：12，13，15，16，17，14，
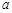
假设所有病人的康复时间互相独立，从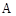，两组随机各选1人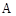，组选出的人记为甲，组选出的人记为乙．
（Ⅰ）求甲的康复时间不少于14天的概率；
（Ⅱ）如果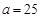
，求甲的康复时间比乙的康复时间长的概率；
（Ⅲ）当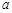为何值时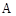，，两组病人康复时间的方差相等？（结论不要求证明）
满足
，
，
，并猜想
的表达式；
的图象经过点（0，-1），且在
处的切线方程是
.
的解析式；
，
，求证：
.
满足
为实数（
为虚数单位），且
，求
，求
的极大值与极小值.推荐套卷
【2015高考北京，理16】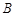，两组各有7位病人，他们服用某种药物后的康复时间（单位：天）记录如下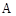：组：10，11，12，13，14，15，16组：12，13，15，16，17，14，
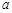
假设所有病人的康复时间互相独立，从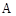，两组随机各选1人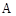，组选出的人记为甲，组选出的人记为乙．
（Ⅰ）求甲的康复时间不少于14天的概率；
（Ⅱ）如果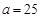，求甲的康复时间比乙的康复时间长的概率；
（Ⅲ）当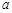为何值时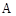，，两组病人康复时间的方差相等？（结论不要求证明）
粤公网安备 44130202000953号