某商店在四个月的试销期内,只销售A、B两个品牌的电视机,共售出400台.试销结束后,只能经销其中的一个品牌,为作出决定,经销人员正在绘制两幅统计图,如图11-1和图11-2.
第四个月销量占总销量的百分比是 ;
在图11-2中补全表示B品牌电视机月销量的折线;

为跟踪调查电视机的使用情况,从该商店第四个月售出的电视机中,随机抽取一台,求抽到B品牌电视机的概率
经计算,两个品牌电视机月销量的平均水平相同,请你结合折线的走势进行简要分析,判断该商店应经销哪个品牌的电视机.
相关知识点
推荐套卷
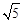 .由此可知新正方形边长等于两个小正方形组成的矩形的对角线长.
.由此可知新正方形边长等于两个小正方形组成的矩形的对角线长.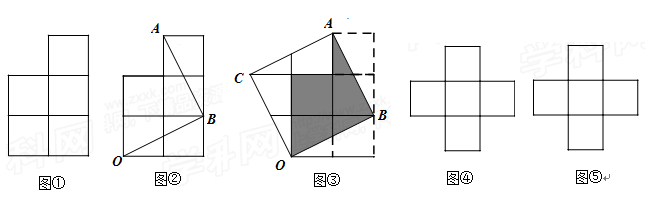
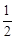 ∠ACB;
∠ACB; ,CB=12,求⊙O 的半径及
,CB=12,求⊙O 的半径及 的值.
的值.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号