为了让学生了解文明礼仪知识,增强文明意识,养成文明习惯。某中学在“文明礼仪,从我做起”知识普及活动中,举行了一次“文明礼仪知识”竞赛,共有3000名学生参加了这次竞赛。为了了解本次竞赛的成绩情况,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行了统计。
频率分布表
组别
|
分组
|
频数
|
频率
|
1
|
50.5~60.5
|
6
|
0.08
|
2
|
60.5~70.5
|
9
|
0.12
|
3
|
70.5~80.5
|
15
|
m
|
4
|
80.5~90.5
|
24
|
0.32
|
5
|
90.5~100.5
|
n
|
0.28
|
合计
|
|
|
|
频数分布直方图
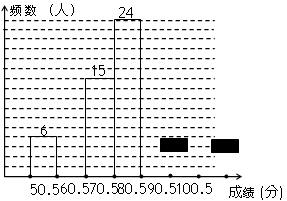
请你根据上面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
(1)求频率分布表中的m、n;
(2)补全频数分布直方图;
(3)你能根据所学知识确定“众数”落在哪一组吗?“中位数”在哪一组吗?