(本题10分)近几年后,实验中学准备搬迁新校舍,在迁入新校舍之前,同学们就学校学生如何到校问题进行了一次调查,并将调查结果制成了表格、条形图和扇形统计图,请你根据图表信息完成下列各题: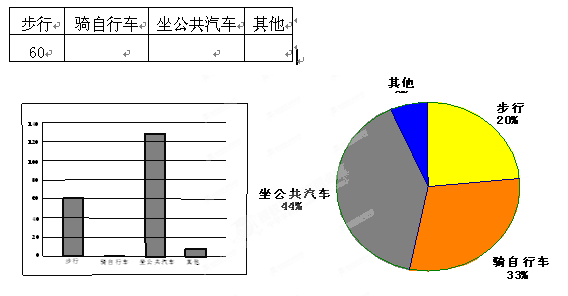
(1)此次共调查了多少位学生?
(2)请将表格填充完整;
(3)请将条形统计图补充完整.
相关知识点
推荐套卷
(本题10分)近几年后,实验中学准备搬迁新校舍,在迁入新校舍之前,同学们就学校学生如何到校问题进行了一次调查,并将调查结果制成了表格、条形图和扇形统计图,请你根据图表信息完成下列各题:
(1)此次共调查了多少位学生?
(2)请将表格填充完整;
(3)请将条形统计图补充完整.