如图为河岸一段的示意图.一游泳者站在河岸的A点处,欲前往对岸的C点处,若河宽BC为100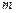 ,A、B相距100
,A、B相距100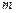 ,他希望尽快到达C,准备从A步行到E(E为河岸AB上的点),再从E游到C.已知此人步行速度为
,他希望尽快到达C,准备从A步行到E(E为河岸AB上的点),再从E游到C.已知此人步行速度为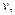 游泳速度为
游泳速度为 .
.
(1)设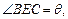 试将此人按上述路线从A到C所需时间T表示为
试将此人按上述路线从A到C所需时间T表示为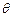 的函数,并求自变量
的函数,并求自变量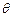 的取值范围;
的取值范围;
(2)当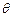 为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?
为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?
推荐套卷
如图为河岸一段的示意图.一游泳者站在河岸的A点处,欲前往对岸的C点处,若河宽BC为100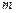 ,A、B相距100
,A、B相距100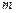 ,他希望尽快到达C,准备从A步行到E(E为河岸AB上的点),再从E游到C.已知此人步行速度为
,他希望尽快到达C,准备从A步行到E(E为河岸AB上的点),再从E游到C.已知此人步行速度为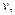 游泳速度为
游泳速度为 .
.
(1)设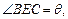 试将此人按上述路线从A到C所需时间T表示为
试将此人按上述路线从A到C所需时间T表示为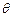 的函数,并求自变量
的函数,并求自变量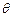 的取值范围;
的取值范围;
(2)当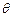 为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?
为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?