(本小题满分14分)
已知函数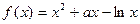 ,
, 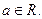
(Ⅰ)若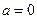 时,求曲线
时,求曲线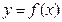 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若函数 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(Ⅲ)令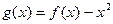 ,是否存在实数
,是否存在实数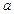 ,当
,当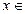
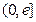 (
( 是自然对数的底)时,函数
是自然对数的底)时,函数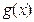 的最小值是3,若存在,求出
的最小值是3,若存在,求出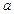 的值;若不存在,说明理由.
的值;若不存在,说明理由.
推荐套卷
(本小题满分14分)
已知函数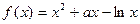 ,
, 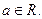
(Ⅰ)若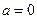 时,求曲线
时,求曲线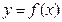 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若函数 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(Ⅲ)令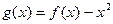 ,是否存在实数
,是否存在实数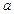 ,当
,当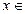
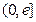 (
( 是自然对数的底)时,函数
是自然对数的底)时,函数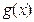 的最小值是3,若存在,求出
的最小值是3,若存在,求出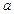 的值;若不存在,说明理由.
的值;若不存在,说明理由.