(本小题13分)
一个多面体的直观图和三视图如图所示,其中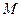 ,
, 分别是
分别是 ,
, 的中点,
的中点, 是
是 上的一动点.
上的一动点.
(Ⅰ)求该几何体的体积与表面积;
(Ⅱ)求证: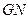 ⊥
⊥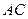 ;
;
(Ⅲ)当 时,在棱
时,在棱 上确定一点
上确定一点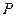 ,使得
,使得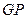 //平面
//平面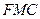 ,并给出证明.
,并给出证明.
推荐套卷
(本小题13分)
一个多面体的直观图和三视图如图所示,其中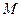 ,
, 分别是
分别是 ,
, 的中点,
的中点, 是
是 上的一动点.
上的一动点.
(Ⅰ)求该几何体的体积与表面积;
(Ⅱ)求证: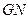 ⊥
⊥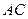 ;
;
(Ⅲ)当 时,在棱
时,在棱 上确定一点
上确定一点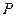 ,使得
,使得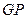 //平面
//平面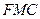 ,并给出证明.
,并给出证明.