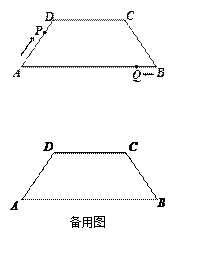
（本题8分）在等腰梯形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=13，点P从点A出发以每秒2个单位长度的速度沿AD→DC向终点C运动，同时点Q从点B出发，以每秒1个单位的速度沿BA向终点A运动，设运动时间为t秒.
⑴当t为何值时，四边形PQBC为平行四边形时？
⑵在整个运动过程中，当t为何值时，以点C、P、Q为顶点的三角形是直角三角形？
 |
相关试题
，最大角是
,求这个多边形的边数.
，中间空一个小正方形面积为
,求长方形瓷砖的长和宽.
∠
∠
∠
∠
∠
的度数.
相关知识点
推荐套卷
（本题8分）在等腰梯形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=13，点P从点A出发以每秒2个单位长度的速度沿AD→DC向终点C运动，同时点Q从点B出发，以每秒1个单位的速度沿BA向终点A运动，设运动时间为t秒.
⑴当t为何值时，四边形PQBC为平行四边形时？
⑵在整个运动过程中，当t为何值时，以点C、P、Q为顶点的三角形是直角三角形？
|
粤公网安备 44130202000953号