如图1和图2，△ ABC中，∠BAC=90°，AB=AC，AD⊥BC，垂足是D，AE平分∠BAD，交BC于点E．过点A作AF⊥AE，过点C作CF∥AD，两直线交于点F．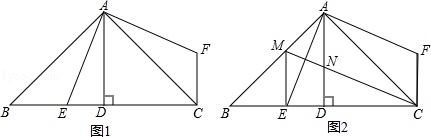
（1）在图1中，证明：△ACF≌△ABE；
（2）在图2中，∠ACB的平分线交AB于点M，交AD于点N．
①求证：四边形ANCF是平行四边形；
②求证：ME=MA；
③四边形ANCF是不是菱形？若是，请证明；若不是，请简要说明理由．
，其中m=5．
，其中m=3，n=4．相关知识点
推荐套卷
如图1和图2，△ ABC中，∠BAC=90°，AB=AC，AD⊥BC，垂足是D，AE平分∠BAD，交BC于点E．过点A作AF⊥AE，过点C作CF∥AD，两直线交于点F．
（1）在图1中，证明：△ACF≌△ABE；
（2）在图2中，∠ACB的平分线交AB于点M，交AD于点N．
①求证：四边形ANCF是平行四边形；
②求证：ME=MA；
③四边形ANCF是不是菱形？若是，请证明；若不是，请简要说明理由．
粤公网安备 44130202000953号