(本小题满分12分)
已知函数 ,且函数
,且函数 的最小正周期
的最小正周期
为
(1)若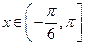 ,求函数
,求函数 的单调递减区间;
的单调递减区间;
(2)将函数 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的 ,把所得到的图象再向左平移
,把所得到的图象再向左平移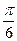 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 在区间
在区间 上的最小值。
上的最小值。
推荐套卷
(本小题满分12分)
已知函数 ,且函数
,且函数 的最小正周期
的最小正周期
为
(1)若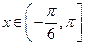 ,求函数
,求函数 的单调递减区间;
的单调递减区间;
(2)将函数 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的 ,把所得到的图象再向左平移
,把所得到的图象再向左平移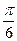 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 在区间
在区间 上的最小值。
上的最小值。