（本小题满分12分．其中（Ⅰ）小问6分，（Ⅱ）小问6分）
如图，已知四棱锥P-ABCD的底面ABCD是边长为2的正方形，PD⊥底面ABCD，E、F分别为棱BC、AD的中点．
（Ⅰ）若PD=1，求异面直线PB和DE所成角的余弦值；
（Ⅱ）若二面角P-BF-C的余弦值为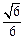
，求四棱锥P-ABCD的体积
.
；
，求实数a.
（Ⅰ）判断
的奇偶性；（Ⅱ）求
（其值用
表示）
是奇函数，且
时
则
的前
项和
满足：
，数列
满足：对任意
有
.
，数列
的前
项和为
，证明：当
时，
．推荐套卷
（本小题满分12分．其中（Ⅰ）小问6分，（Ⅱ）小问6分）
如图，已知四棱锥P-ABCD的底面ABCD是边长为2的正方形，PD⊥底面ABCD，E、F分别为棱BC、AD的中点．
（Ⅰ）若PD=1，求异面直线PB和DE所成角的余弦值；
（Ⅱ）若二面角P-BF-C的余弦值为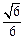，求四棱锥P-ABCD的体积
粤公网安备 44130202000953号