某厂家拟在2010年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)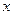 万件与促销费用
万件与促销费用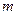 万元(
万元( )满足
)满足 (
( 为常数),如果不搞促销活动,则该产品的年销量只能是1万件。已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品的年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)。
为常数),如果不搞促销活动,则该产品的年销量只能是1万件。已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品的年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)。
(1)将2010年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2010年的促销费用投入多少万元时,厂家的利润最大?
推荐套卷
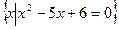 ,B=
,B=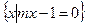 ,且
,且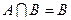 ,求由实数
,求由实数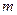 所构成的集合
所构成的集合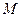 ,并写出
,并写出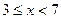 }, B={
}, B={ }, C={
}, C={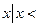 a}
a} (2)求
(2)求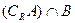 ;(3)若
;(3)若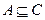 ,求a的取值范围.
,求a的取值范围.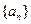 满足,
满足,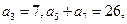
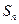 。(1)求
。(1)求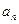 和
和
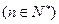 ,求数列
,求数列 的前n项和
的前n项和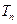
 中,角
中,角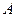 、
、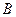 、
、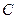 对的边分别为
对的边分别为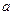 、
、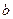 、
、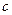 ,且满足:
,且满足: ,
, 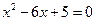 的两根。
的两根。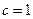 ,求
,求 是等差数列,且
是等差数列,且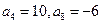
 为
为 粤公网安备 44130202000953号
粤公网安备 44130202000953号