如图,△ABC是等边三角形,其中A点的坐标是(0,6),C点的坐标是(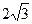 ,0),B点在x轴上。
,0),B点在x轴上。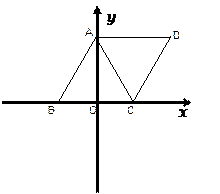
写出B点的坐标;
线段AB向右平移,点A、B分别平移至点D、C位置,得到平行四边形ABCD。求这个平行四边形的面积;
如果以点A、B、C作为平行四边形的顶点,那么另外一点(除D点外)的坐标是什么?(不用写计算过程,直接写答案)
相关知识点
推荐套卷
如图,△ABC是等边三角形,其中A点的坐标是(0,6),C点的坐标是(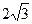 ,0),B点在x轴上。
,0),B点在x轴上。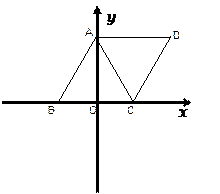
写出B点的坐标;
线段AB向右平移,点A、B分别平移至点D、C位置,得到平行四边形ABCD。求这个平行四边形的面积;
如果以点A、B、C作为平行四边形的顶点,那么另外一点(除D点外)的坐标是什么?(不用写计算过程,直接写答案)