已知幂函数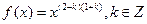
，且
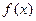在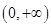
上单调递增.
（Ⅰ）求实数
的值，并写出相应的函数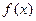的解析式；
（II）若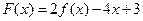
在区间
上不单调，求实数
的取值范围；
（III）试判断是否存在正数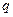
，使函数
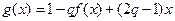在区间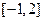
上的值域为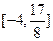
. 若存在，求出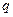的值；若不存在，请说明理由
，若对于任意的
，
,且
，求证：存在
使得
>0时，
=
>
恒成立，求正整数
的最大值
是定义在
上的单调递增函数，对于任意的
满足
，且
满足
，
，
，并猜想
，进一步归纳出更一般的结论
，
，
均为正数，且
+
+
推荐套卷
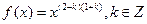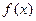已知幂函数，且在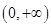上单调递增.
（Ⅰ）求实数的值，并写出相应的函数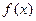的解析式；
（II）若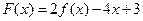在区间上不单调，求实数的取值范围；
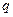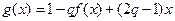（III）试判断是否存在正数，使函数在区间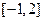上的值域为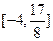. 若存在，求出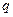的值；若不存在，请说明理由
粤公网安备 44130202000953号