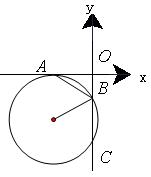
如图,平面直角坐标系中,⊙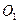 与
与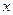 轴相切于点
轴相切于点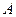 ,与
,与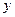 轴相交于点
轴相交于点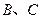 两点,连结
两点,连结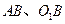 。
。
(1)求证
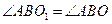 ;
;(2)若点
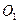 的坐标为
的坐标为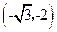 ,直接写出点
,直接写出点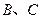 的坐标
的坐标(3)在(2)的条件下,过
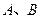 两点作⊙
两点作⊙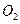 与
与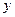 轴的正半轴交于点
轴的正半轴交于点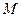 ,与
,与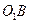 的延长线交于点
的延长线交于点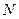 ,当⊙
,当⊙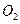 的大小变化时,给出下列两个结论:
的大小变化时,给出下列两个结论: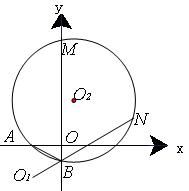
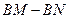 的值不变;②
的值不变;②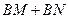 的值不变;
的值不变;
其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值。
相关知识点
推荐套卷
如图,平面直角坐标系中,⊙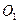 与
与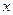 轴相切于点
轴相切于点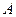 ,与
,与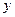 轴相交于点
轴相交于点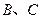 两点,连结
两点,连结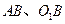 。
。
(1)求证
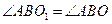 ;
;(2)若点
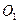 的坐标为
的坐标为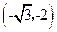 ,直接写出点
,直接写出点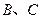 的坐标
的坐标(3)在(2)的条件下,过
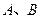 两点作⊙
两点作⊙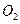 与
与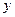 轴的正半轴交于点
轴的正半轴交于点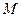 ,与
,与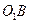 的延长线交于点
的延长线交于点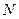 ,当⊙
,当⊙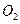 的大小变化时,给出下列两个结论:
的大小变化时,给出下列两个结论:
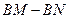 的值不变;②
的值不变;②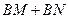 的值不变;
的值不变;
其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值。