如图，某人在塔的正东方向上的C处在与塔垂直的水平面内沿南偏西60°的方向以每小时6千米的速度步行了1分钟以后，在点D处望见塔的底端B在东北方向上，已知沿途塔的仰角
,的最大值为
．
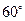（1）求该人沿南偏西60°的方向走到仰角最大时，走了几分钟；
（2）求塔的高AB.
相关试题
中，点
到两点
的距离之和为4，设点
,直线
与
两点。
，求
的值。
有共同焦点，且过点(0,2)的双曲线方程，并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程.
，
，若
是
的必要不充分条件，求实数
的取值范围．）相关知识点
推荐套卷
如图，某人在塔的正东方向上的C处在与塔垂直的水平面内沿南偏西60°的方向以每小时6千米的速度步行了1分钟以后，在点D处望见塔的底端B在东北方向上，已知沿途塔的仰角,的最大值为．
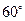（1）求该人沿南偏西60°的方向走到仰角最大时，走了几分钟；
（2）求塔的高AB.
粤公网安备 44130202000953号