(满分l2分)某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25 min,于是立即步行回家取票.同时,他父亲从家里骑自行车出发以小明3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.图中线段AB,OB分别表示父子俩送票、取票的过程中,离体育馆的路程5 m与所用时间t min之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(1)求点B的坐标和AB所在直线的函数关系式;
(2)小明能否在比赛开始前到达体育馆?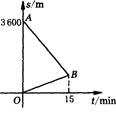
相关知识点
推荐套卷
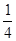 .那么每天最多获利多少元,最少获利多少元?获利最多的方案如何设计?
.那么每天最多获利多少元,最少获利多少元?获利最多的方案如何设计?
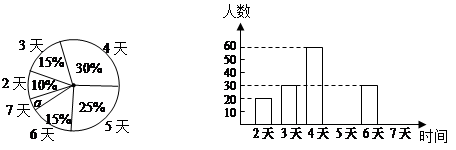
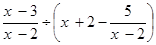 ,其中
,其中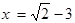 。
。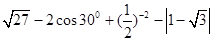
 粤公网安备 44130202000953号
粤公网安备 44130202000953号