（本小题满分１２分）如图，两个同心圆的圆心是O，大圆的半径为13，小圆的半径为5，AD是大圆的直径．大圆的弦AB，BE分别与小圆相切于点C，F．AD，BE相交于点G，连接BD．
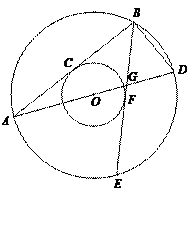
（1）求BD的长；
（2）求∠ABE+2∠D的度数；
（3）求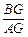
的值．
+|b3－27|=0，求(a－b)b的立方根.
相关知识点
推荐套卷
（本小题满分１２分）如图，两个同心圆的圆心是O，大圆的半径为13，小圆的半径为5，AD是大圆的直径．大圆的弦AB，BE分别与小圆相切于点C，F．AD，BE相交于点G，连接BD．
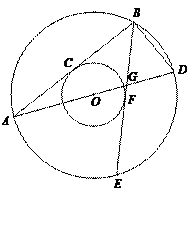
（1）求BD的长；
（2）求∠ABE+2∠D的度数；
（3）求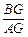的值．
粤公网安备 44130202000953号