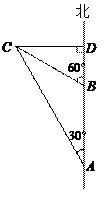（本小题满分8分）
如图，一艘轮船以每小时20海里的速度沿正北方向航行，在A处测得灯塔C在北偏西30°方向，轮船航行2小时后到达B处，在B处测得灯塔C在北偏西60°方向．当轮船到达灯塔C的正东方向的D处时，求此时轮船与灯塔C的距离．（结果保留根号）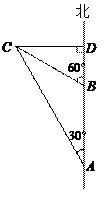
与
的大小，并说明理由；
与
的和为多少度？为什么？
的相反数为
，
的倒数为
，
的绝对值为2，求
的值．
其中
=－3．
－
）＋32 
相关知识点
推荐套卷
粤ICP备20024846号
粤公网安备 44130202000953号
粤公网安备 44130202000953号
Copyright ©2020-2024 优题课 youtike.com 版权所有
Powered by：Youtike Platform 6.6.2
声明：本网站部分内容由互联网用户自发贡献自行上传，本网站不拥有所有权，也不承担相关法律责任。
如果您发现有涉嫌版权的内容，欢迎发送邮件至：service@youtike.com 或 联系QQ：267757 进行举报，一经查实，本站将立刻删除涉嫌侵权内容。
如果您发现有涉嫌版权的内容，欢迎发送邮件至：service@youtike.com 或 联系QQ：267757 进行举报，一经查实，本站将立刻删除涉嫌侵权内容。