若矩形的一个短边与长边的比值为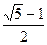 ,(黄金分割数),我们把这样的矩形叫做黄金矩形
,(黄金分割数),我们把这样的矩形叫做黄金矩形
(1) 操作:请你在如图15所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD。
(2) 探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由。
(3) 归纳:通过上述操作及探究,请概括出具体有一般性的结论(不需证明)
相关知识点
推荐套卷
若矩形的一个短边与长边的比值为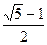 ,(黄金分割数),我们把这样的矩形叫做黄金矩形
,(黄金分割数),我们把这样的矩形叫做黄金矩形
(1) 操作:请你在如图15所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD。
(2) 探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由。
(3) 归纳:通过上述操作及探究,请概括出具体有一般性的结论(不需证明)