某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径.下图是水平放置的破裂管道有水部分的截面.
(1)作图题:请你用圆规、直尺作出这个输水管道的圆形截面的圆心;(不写作法,保留作图痕迹)
(2)若这个输水管道有水部分的水面宽AB=8,水面最深的地方的高度为2,求这个圆形截面的半径.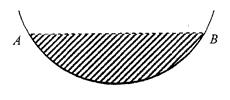
相关知识点
推荐套卷
某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径.下图是水平放置的破裂管道有水部分的截面.
(1)作图题:请你用圆规、直尺作出这个输水管道的圆形截面的圆心;(不写作法,保留作图痕迹)
(2)若这个输水管道有水部分的水面宽AB=8,水面最深的地方的高度为2,求这个圆形截面的半径.