如图，港口B位于港口O正西方向120海里处，小岛C位于港口O北偏西60°的方向．一艘科学考察船从港口O出发，沿北偏西30°的OA方向以20海里/小时的速度驶离港口O．同时一艘快艇从港口B出发，沿北偏东30°的方向以60海里/小时的速度驶向小岛C，在小岛C用1小时装补给物资后，立即按原来的速度给考察船送去．
（1）快艇从港口B到小岛C需要多少时间？
（2）快艇从小岛C出发后最少需要多少时间才能和考察船相遇？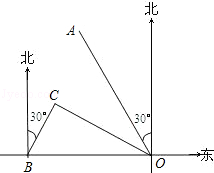
相关试题
时，有最大值
，且当x=0时，y= 
（2）、（x+3）（x-6）=
某商场将进价为30元的台灯按40元出售，平均每月能售出600盏。调查表明，这种台灯的售价每上涨1元，其销售量减少10盏。为了实现平均每月10000元的销售利润，这种台灯的售价应定为多少元？这时应进台灯多少盏？
如图，二次函数
的图象经过A 、B、C三点．
（1）观察图象，写出A 、B、C三点的坐标，并求出抛物线解析式;
（2）求此抛物线的顶点坐标和对称轴;
（3）观察图象，当x取何值时，y＜0？
的方程
，无论k取任何值，都有两个不相等的实数根．相关知识点
推荐套卷
粤公网安备 44130202000953号