已知关于x的两个一元二次方程：
方程①: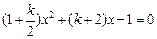 
; 方程②: 
.
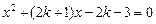（1）若方程①有两个相等的实数根，求解方程②；
（2）若方程①和②中只有一个方程有实数根, 请说明此时哪个方程没有实数根, 并化
简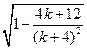
；
（3）若方程①和②有一个公共根a, 求代数式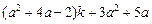
的值．
在实数范围内成立，其中
，
，
是两两不同的实数，求
。
∠CAB．
，求BC和BF的长．
其中
．
，其中
。相关知识点
推荐套卷
已知关于x的两个一元二次方程：
方程①: 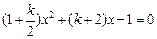; 方程②: .
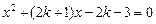（1）若方程①有两个相等的实数根，求解方程②；
（2）若方程①和②中只有一个方程有实数根, 请说明此时哪个方程没有实数根, 并化
简；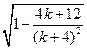
（3）若方程①和②有一个公共根a, 求代数式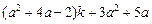的值．
粤公网安备 44130202000953号