如图，现有一块矩形空地，要在这块空地上开辟一个内
接四边形为绿地，使其四个顶点分别落在矩形的四条边上，已知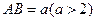
，
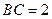，且
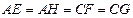，设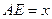
，绿地面积为
.
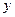1、写出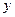关于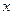
的函数关系式，并指出其定义域；
2、当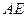
为何值时，绿地面积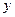最大？
，2tanα＋3sinβ＝7，且tanα－6sinβ＝1，求sinα的值．
－
.
>0；
.
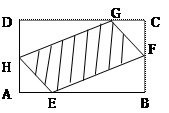
； (2)y＝lg(3－4sin2x)．推荐套卷
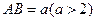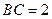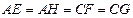如图，现有一块矩形空地，要在这块空地上开辟一个内接四边形为绿地，使其四个顶点分别落在矩形的四条边上，已知，，且，设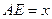，绿地面积为.
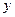1、写出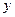关于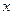的函数关系式，并指出其定义域；
2、当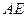为何值时，绿地面积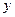最大？
粤公网安备 44130202000953号