如图1,等腰Rt△CEF的斜边CE在正方形ABCD的边BC的延长线上,CF>BC,取线段AE的中点M 。
(1)求证:MD=MF,MD⊥MF(6分)
(2)若Rt△CEF绕点C顺时针旋转任意角度(如图2),其他条件不变。(1)中的结论是否仍然成立,若成立,请证明,若不成立,请说明理由。
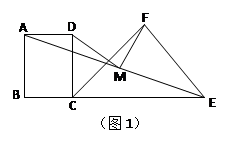 |
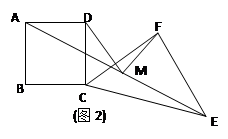 |
||
相关知识点
推荐套卷
如图1,等腰Rt△CEF的斜边CE在正方形ABCD的边BC的延长线上,CF>BC,取线段AE的中点M 。
(1)求证:MD=MF,MD⊥MF(6分)
(2)若Rt△CEF绕点C顺时针旋转任意角度(如图2),其他条件不变。(1)中的结论是否仍然成立,若成立,请证明,若不成立,请说明理由。
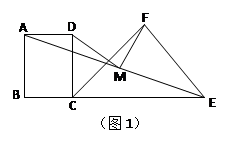 |
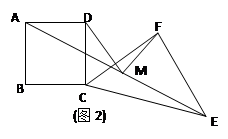 |
||