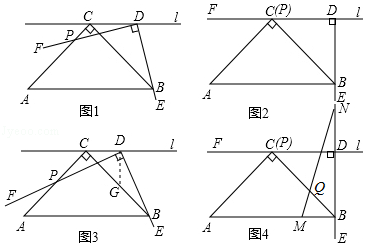
【问题】
如图1,在Rt△ ABC中,∠ ACB=90°, AC= BC,过点 C作直线 l平行于 AB.∠ EDF=90°,点 D在直线 l上移动,角的一边 DE始终经过点 B,另一边 DF与 AC交于点 P,研究 DP和 DB的数量关系.
【探究发现】
(1)如图2,某数学兴趣小组运用"从特殊到一般"的数学思想,发现当点 D移动到使点 P与点 C重合时,通过推理就可以得到 DP= DB,请写出证明过程;
【数学思考】
(2)如图3,若点 P是 AC上的任意一点(不含端点 A、 C),受(1)的启发,这个小组过点 D作 DG⊥ CD交 BC于点 G,就可以证明 DP= DB,请完成证明过程;
【拓展引申】
(3)如图4,在(1)的条件下, M是 AB边上任意一点(不含端点 A、 B), N是射线 BD上一点,且 AM= BN,连接 MN与 BC交于点 Q,这个数学兴趣小组经过多次取 M点反复进行实验,发现点 M在某一位置时 BQ的值最大.若 AC= BC=4,请你直接写出 BQ的最大值.