某校组织学生到恩格贝 A和康镇 B进行研学活动，澄澄老师在网上查得， A和 B分
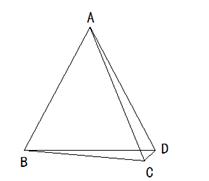
别位于学校 D的正北和正东方向， B位于 A南偏东37°方向，校车从 D出发，沿正北方向前往 A地，行驶到15千米的 E处时，导航显示，在 E处北偏东45°方向有一服务区 C，且 C位于 A， B两地中点处．
（1）求 E， A两地之间的距离；
（2）校车从 A地匀速行驶1小时40分钟到达 B地，若这段路程限速100千米/时，计算校车是否超速？
（参考数据：sin37°＝ ，cos37°＝ ，tan37°＝ ）
相关试题
用反例来证明下列命题是假命题．
（1）若xy=0，则x，y同时为零；（2）两个负数的差一定是负数；
（3）两个锐角的和一定大于直角；（4）任何有理数都有倒数．
在四边形ABCD中，∠A=∠B，∠C=∠ADC．
（1）求证：AB∥CD．
（2）若∠ADC-∠A=60°，过点D作DE∥BC交AB于点E．请判断△ADE是哪种特殊三角形，并说明理由．
相关知识点
推荐套卷
粤公网安备 44130202000953号