(本小题满分l2分)
在“环境保护低碳生活知识竞赛”第一环节测试中,设有A、B、C三道必答题,分值依次为20分、30分、50分.竞赛规定:若参赛选手连续两道题答题错误,则必答题总分记为零分;否则各题得分之和记为必答题总分.已知某选手回答A、B、C三道题正确的概率分别为 、
、 、
、 ,且回答各题时相互之间没有影响.
,且回答各题时相互之间没有影响.
(1) 若此选手可以自由选择答题顺序,求其必答题总分为50分的概率;
(2) 若此选手按A、B、C的顺序答题,求其必答题总分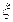 的分布列和数学期望.
的分布列和数学期望.
相关知识点
推荐套卷
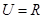 ,函数
,函数 的定义域为A,函数
的定义域为A,函数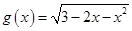 的值域为B,求
的值域为B,求 和
和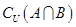
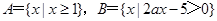 ,
,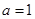 ,求
,求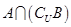 .
.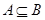 ,求
,求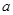 的取值范围。
的取值范围。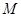 :
: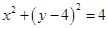 ,点
,点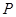 是直线
是直线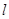 :
: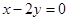 上的一动点,过点
上的一动点,过点 、
、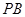 ,切点为
,切点为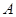 、
、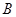 .
.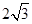 时,求点
时,求点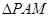 的外接圆为圆
的外接圆为圆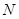 ,试问:当
,试问:当 长度的最小值.
长度的最小值. ,且
,且 ,
, 为线段PC上一点.
为线段PC上一点.
 时,证明:
时,证明: ;
; ,证明:
,证明:
 ,若存在,请确定点
,若存在,请确定点 粤公网安备 44130202000953号
粤公网安备 44130202000953号