(本题满分12分,(Ⅰ)小问4分,(Ⅱ)小问6分,(Ⅲ)小问2分.)
如图所示,直二面角 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
,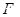 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
(Ⅰ)求证: ⊥平面
⊥平面
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求点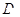 到平面
到平面 的距离.
的距离.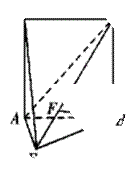
推荐套卷
(本题满分12分,(Ⅰ)小问4分,(Ⅱ)小问6分,(Ⅲ)小问2分.)
如图所示,直二面角 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
,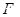 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
(Ⅰ)求证: ⊥平面
⊥平面
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求点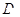 到平面
到平面 的距离.
的距离.