供电局的电力维修工甲、乙两人要到45千米远的A地进行电力抢修.甲骑摩托车先行,t(t≥0)小时后乙开抢修车载着所需材料出发.
(1). 若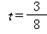 (小时),抢修车的速度是摩托车的1.5倍,且甲、乙两人同时到达,求摩托车的速度;
(小时),抢修车的速度是摩托车的1.5倍,且甲、乙两人同时到达,求摩托车的速度;
(2). 若摩托车的速度是45千米/小时,抢修车的速度是60千米/小时,且乙不能比甲晚到,则t的最大值是多少?
供电局的电力维修工甲、乙两人要到45千米远的A地进行电力抢修.甲骑摩托车先行,t(t≥0)小时后乙开抢修车载着所需材料出发.
(1). 若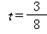 (小时),抢修车的速度是摩托车的1.5倍,且甲、乙两人同时到达,求摩托车的速度;
(小时),抢修车的速度是摩托车的1.5倍,且甲、乙两人同时到达,求摩托车的速度;
(2). 若摩托车的速度是45千米/小时,抢修车的速度是60千米/小时,且乙不能比甲晚到,则t的最大值是多少?