如图,Rt△ABC中,∠C=90°,∠A=60°,AC=2.按以下步骤作图: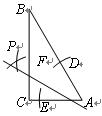
①以A为圆心,以小于AC长为半径画弧,分别交AC、AB于点E、D;
②分别以D、E为圆心,以大于DE长为半径画弧,两弧相交于点P;
③连结AP交BC于点F.那么:
(1)AB的长等于__________(直接填写答案);
(2)∠CAF =_________°(直接填写答案).
相关知识点
推荐套卷
如图,Rt△ABC中,∠C=90°,∠A=60°,AC=2.按以下步骤作图:
①以A为圆心,以小于AC长为半径画弧,分别交AC、AB于点E、D;
②分别以D、E为圆心,以大于DE长为半径画弧,两弧相交于点P;
③连结AP交BC于点F.那么:
(1)AB的长等于__________(直接填写答案);
(2)∠CAF =_________°(直接填写答案).