(本小题满分14分)对于函数 ,若存在
,若存在 ,使
,使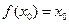 成立,则称
成立,则称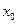 为
为 的不动点。如果函数
的不动点。如果函数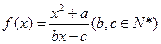 有且仅有两个不动点
有且仅有两个不动点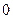 、
、 ,且
,且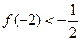 。
。
(1)试求函数 的单调区间;
的单调区间;
(2)已知各项均为负的数列 满足
满足 ,求证:
,求证: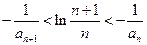 ;
;
(3)设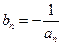 ,
,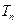 为数列
为数列 的前
的前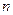 项和,求证:
项和,求证: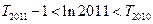 。
。
推荐套卷
(本小题满分14分)对于函数 ,若存在
,若存在 ,使
,使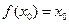 成立,则称
成立,则称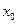 为
为 的不动点。如果函数
的不动点。如果函数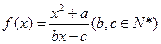 有且仅有两个不动点
有且仅有两个不动点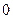 、
、 ,且
,且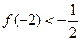 。
。
(1)试求函数 的单调区间;
的单调区间;
(2)已知各项均为负的数列 满足
满足 ,求证:
,求证: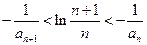 ;
;
(3)设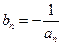 ,
,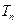 为数列
为数列 的前
的前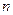 项和,求证:
项和,求证: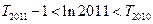 。
。