某班为了从甲、乙两位同学中选出班长,进行了一次演讲答辩与民主测评 ,A、
,A、
B、C、D、E五位老师作为评委,对“演讲答辩”情况进行评价,全班50位同学参与了 民
民
主测评。结果如下表所示: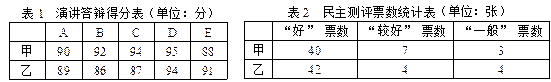
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分综合得分=演讲答辩得分×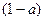 +民主测评得分×
+民主测评得分× (0.5≤
(0.5≤ ≤0.8)如果以综合得分来确定班长,试问:甲、乙两位同学哪一位当选为班长?并说明理由。
≤0.8)如果以综合得分来确定班长,试问:甲、乙两位同学哪一位当选为班长?并说明理由。
相关知识点
推荐套卷


 B
B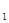 ;
; B
B =0.
=0.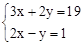
 粤公网安备 44130202000953号
粤公网安备 44130202000953号