（本小题满分12分）在平面直角坐标系xOy中,有一个以为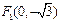
和
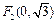焦点、离心率为
的椭圆.设椭圆在第一象限的部分为曲线C, 动点P在C上, C在点P处
的切线与x , y轴的交点分别为A、B,且向量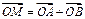
.求:
（1）点M的轨迹方程；
（2）
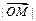的最小值.
的大小
若
，求a的取值范围
>3推荐套卷
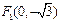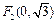（本小题满分12分）在平面直角坐标系xOy中,有一个以为和焦点、离心率为的椭圆.设椭圆在第一象限的部分为曲线C, 动点P在C上, C在点P处
的切线与x , y轴的交点分别为A、B,且向量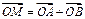.求:
（1）点M的轨迹方程；
（2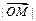）的最小值.
粤公网安备 44130202000953号