(本小题8分)为贯彻落实云南省教育厅提出的“三生教育”,在母亲节来临之际,某校团委组织了以“珍爱生命,学会生存,感恩父母”为主题的教育活动,在学校随机调查了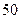 名同学平均每周在家做家务的时间,统计并制作了如下的频数分布和扇形统计图:
名同学平均每周在家做家务的时间,统计并制作了如下的频数分布和扇形统计图:

根据上述信息回答下列问题:
 ,
, ;
; 在扇形统计图中,
在扇形统计图中, 组所占圆心角的度数为 ;
组所占圆心角的度数为 ; 全校共有
全校共有 名学生,估计该校平均每周做家务时间不少于
名学生,估计该校平均每周做家务时间不少于 小时的学生约有多少人?
小时的学生约有多少人?
相关知识点
推荐套卷
(本小题8分)为贯彻落实云南省教育厅提出的“三生教育”,在母亲节来临之际,某校团委组织了以“珍爱生命,学会生存,感恩父母”为主题的教育活动,在学校随机调查了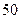 名同学平均每周在家做家务的时间,统计并制作了如下的频数分布和扇形统计图:
名同学平均每周在家做家务的时间,统计并制作了如下的频数分布和扇形统计图:

根据上述信息回答下列问题:
 ,
, ;
; 在扇形统计图中,
在扇形统计图中, 组所占圆心角的度数为 ;
组所占圆心角的度数为 ; 全校共有
全校共有 名学生,估计该校平均每周做家务时间不少于
名学生,估计该校平均每周做家务时间不少于 小时的学生约有多少人?
小时的学生约有多少人?