如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).
⑴ 在如图⑵建立的坐标系下,求网球飞行路线的抛物线解析式.
⑵ 若竖直摆放5个圆柱形桶时,则网球能落入桶内吗?说明理由;
⑶若要使网球能落入桶内,求竖直摆放的圆柱形桶的个数.
相关知识点
推荐套卷
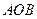 中,
中,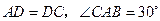 ,
,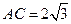 ,求
,求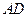 的长度.
的长度.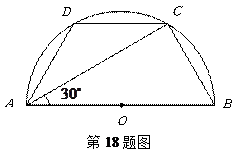
 拟台球游戏,为简单起见,约定:①每个球袋视为一个点,如果不遇到障碍,各球均沿直线前进;②A球击B球,意味着B球在A球前进的路线上,且B球被撞击后沿A球原来的方向前进;③球撞击桌边后的反弹角度等于入射角度,(如图中∠β=∠a)如图所示,设桌边只剩下白球,A,6号球B。
拟台球游戏,为简单起见,约定:①每个球袋视为一个点,如果不遇到障碍,各球均沿直线前进;②A球击B球,意味着B球在A球前进的路线上,且B球被撞击后沿A球原来的方向前进;③球撞击桌边后的反弹角度等于入射角度,(如图中∠β=∠a)如图所示,设桌边只剩下白球,A,6号球B。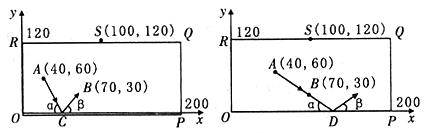

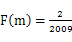 时,求m的值和这m个数的积。
时,求m的值和这m个数的积。 粤公网安备 44130202000953号
粤公网安备 44130202000953号