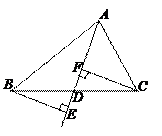如图,已知BE⊥AD,CF⊥ AD,且BE=CF.
AD,且BE=CF.
(1)请你判断AD是△ABC的中线还是角平分线?证明你的结论.
(2)连接BF、CE,能否找到一个条件使四边形BFCE是菱形?直接写出答案: . (填“能”或“不能”)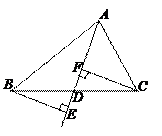

相关知识点
推荐套卷
如图,已知BE⊥AD,CF⊥ AD,且BE=CF.
AD,且BE=CF.
(1)请你判断AD是△ABC的中线还是角平分线?证明你的结论.
(2)连接BF、CE,能否找到一个条件使四边形BFCE是菱形?直接写出答案: . (填“能”或“不能”)