高校招生是根据考生所填报的志愿,从考试成绩所达到的最高第一志愿开始,按顺序分批录取,若前一志愿不能录取,则依次给下一个志愿(同批或下一批)录取.某考生填报了三批共6个不同志愿(每批2个),并对各志愿的单独录取以及能考上各批分数线的概率进行预测,结果如“表一”所示(表中的数据为相应的概率,a、b分别为第一、第二志愿).
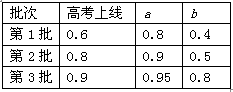
(Ⅰ)求该考生能被第2批b志愿录取的概率;
(Ⅱ)求该考生能被录取的概率;
(Ⅲ)如果已知该考生高考成绩已达到第2批分数线却未能达到第1批分数线,请计算其最有可能在哪个志愿被录取?
(以上结果均保留二个有效数字)